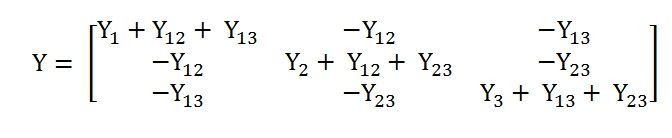In a power system, Bus Admittance Matrix represents the nodal admittances of the various buses. With the help of the transmission line, each bus is connected to the various other buses. Admittance matrix is used to analyse the data that is needed in the load or a power flow study of the buses. It explains the admittance and the topology of the network. The following are the advantages of the bus admittance matrix.
- The data preparation of the bus admittance matrix is very simple.
- The formation of the bus admittance matrix and their modification is easy.
- The bus admittance matrix is a sparse matrix thus the computer memory requirement is less.
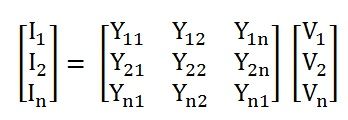The amount of current present in the bus can be calculated with the help of formation of the Admittance matrix. It is expressed as shown above.
In the simplest form, the above matrix can be written as shown below.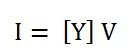
Where,
- I is the current of the bus in the vector form.
- Y is the admittance matrix
- V is the vector of the bus voltage.
Let us consider the figure given below.
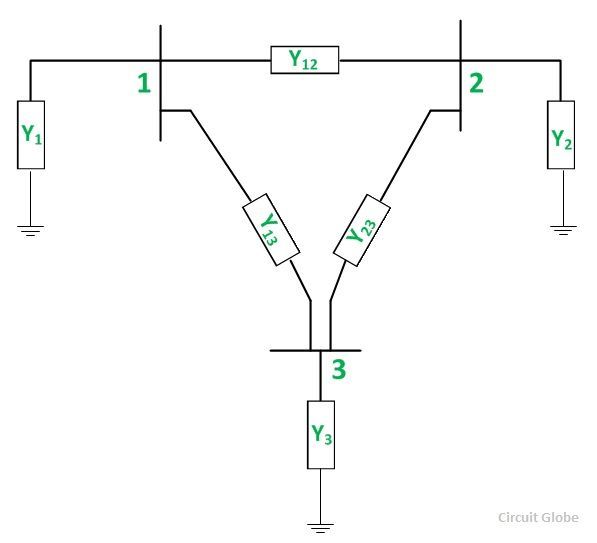From the above figure, the (3×3) admittance matrix is formed as shown below.
The diagonal elements of the Bus Admittance matrix are known as self-admittances and the off-diagonal elements are known as mutual admittances.
Steps for Solving Bus Admittance Matrix
The following steps given below are used to solve the Admittance Matrix.
- First of all, form the bus Admittance matrix.
- Select the reference bus to solve the network.
- Define the known variables for all the other types of buses.
- Assign the initial values for the voltage and angle for all the buses.
- Calculate the power mismatch vector and power injection current.
- Apply the various iteration methods like Newton-Raphson, Gauss-Siedel etc.
- Check the mismatching vector that whether it is within the prescribed limit of 0.001 per unit. If yes, then stop the procedure and if no then continues the steps of iteration to obtain the new values.
- Recheck the values again, whether the obtain values are within the limit.