Superposition theorem states that in any linear, active, bilateral network having more than one source, the response across any element is the sum of the responses obtained from each source considered separately and all other sources are replaced by their internal resistance. The superposition theorem is used to solve the network where two or more sources are present and connected.
Contents:
In other words, it can be stated as if a number of voltage or current sources are acting in a linear network, the resulting current in any branch is the algebraic sum of all the currents that would be produced in it when each source acts alone while all the other independent sources are replaced by their internal resistances.
It is only applicable to the circuit which is valid for the ohm’s law (i.e., for the linear circuit).
Explanation of Superposition Theorem
Let us understand the superposition theorem with the help of an example. The circuit diagram is shown below consists of two voltage sources V1 and V2.
 First, take the source V1 alone and short circuit the V2 source as shown in the circuit diagram below:
First, take the source V1 alone and short circuit the V2 source as shown in the circuit diagram below:
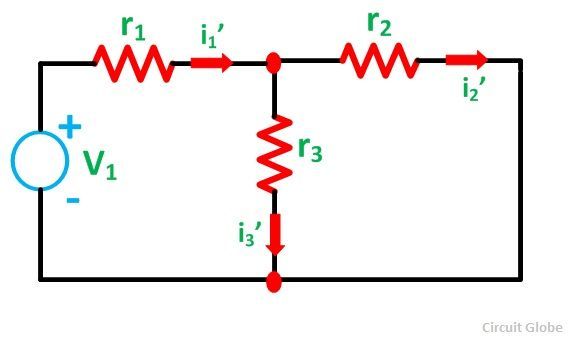 Here, the value of current flowing in each branch, i.e. i1’, i2’ and i3’ is calculated by the following equations.
Here, the value of current flowing in each branch, i.e. i1’, i2’ and i3’ is calculated by the following equations.
The difference between the above two equations gives the value of the current i3’
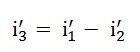
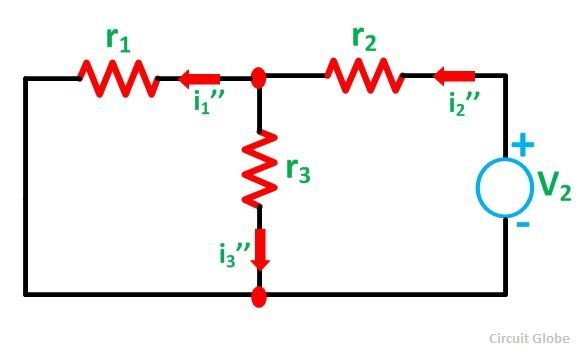
Now, activating the voltage source V2 and deactivating the voltage source V1 by short-circuiting it, find the various currents, i.e. i1’’, i2’’, i3’’ flowing in the circuit diagram shown below:
And the value of the current i3’’ will be calculated by the equation shown below:
![]()
As per the superposition theorem, the value of current i1, i2, i3 is now calculated as:
The direction of the current should be taken care of while finding the current in the various branches.
Steps for Solving network by Superposition Theorem
Considering the circuit diagram A, let us see the various steps to solve the superposition theorem:
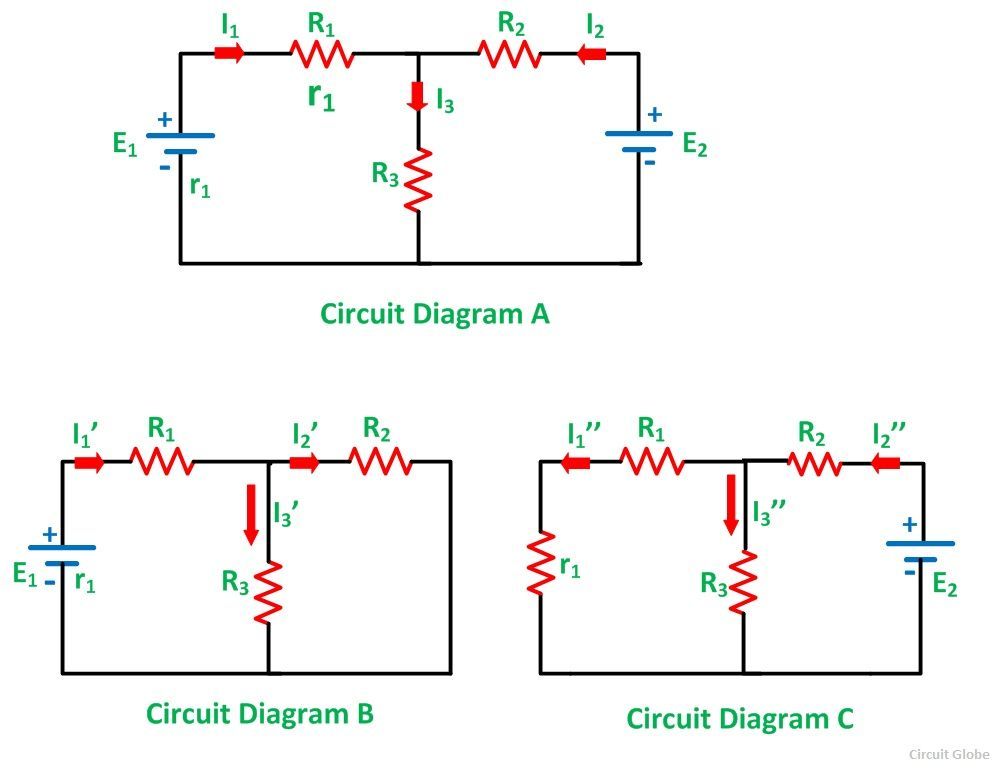 Step 1 – Take only one independent source of voltage or current and deactivate the other sources.
Step 1 – Take only one independent source of voltage or current and deactivate the other sources.
Step 2 – In the circuit diagram B shown above, consider the source E1 and replace the other source E2 by its internal resistance. If its internal resistance is not given, then it is taken as zero and the source is short-circuited.
Step 3 – If there is a voltage source than short circuit it and if there is a current source then just open circuit it.
Step 4 – Thus, by activating one source and deactivating the other source find the current in each branch of the network. Taking the above example find the current I1’, I2’and I3’.
Step 5 – Now consider the other source E2 and replace the source E1 by its internal resistance r1 as shown in the circuit diagram C.
Step 6 – Determine the current in various sections, I1’’, I2’’ and I3’’.
Step 7 – Now to determine the net branch current utilizing the superposition theorem, add the currents obtained from each individual source for each branch.
Step 8 – If the current obtained by each branch is in the same direction then add them and if it is in the opposite direction, subtract them to obtain the net current in each branch.
The actual flow of current in the circuit C will be given by the equations shown below:
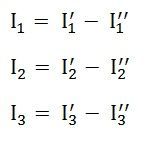
Video: Superposition Theorem
Thus, in this way, we can solve the superposition theorem.

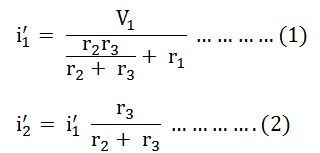
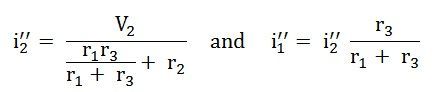
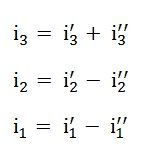
fantastic…
hiii this is kartik, it benefits us to deep study of theorems
Too awesome 👊
Hi,
Nice Tutorial. Keep it up.
very good
Hi, the last equation about I_3 isn’t wrong? It should have been:
I_3 = I’_3 + I”_3
It’s true
i like the steps. It helped me a lot
Did extraordinary work.
many people make this complex.
making simple is special..
The steps are very nice and simple
I have compared the presentations of the Superposition Theorem, the presentation given is the best. This is because the definition of the Superposition theorem is very simple. Secondly the numerical illustration is supportive of the definition.
I am running 83 years and is an Associate Professor of Chemistry now I learn electronics for industrial purposes.
thanks a lot
Fanatics ❣
excellent
Beautifully explained
Amazing tutorials .. thanks
hi my name is sodiq and i am from nigeria
thank you very much for sharing this knowledge.
hello .. I am Midhav, thanks for the wonderful explanation
Nice post
i am very very thankful to you for this wonderful information
Thanks